Readings for 10/24/18
First, there are two kinds of neural networks, those that have recurrent connections and those that don't. A recurrent connection is something like this:
The circle represents a neuron (AKA node; unit) and the arrow represents a connection from the neuron back to itself. Recurrent connections can also be more distant, e.g. from a child neuron to its parent, as long as there is a path that leads back to the originating neuron, e.g. child --> parent --> child.
The important thing to understand about recurrent neural networks is that they are dynamical systems that unfold in time. Imagine that we initialize the neuron above to have a value (AKA energy; activation) of 1 and the recurrent connection to have a strength (AKA weight) of 1. Then the value of the neuron will be constant over time because the energy of the neuron is not being reduced or amplified by the weight of the connection. Alternatively, if the weight was 1.5, then the activation of the neuron would increase over time (1, 1.5, 2.25, ... ), and if the weight was .5, then the activation of the neuron would decrease over time (1, .5, .25, ...). These are positive and negative feedback loops, respectively. To calculate the value of the neuron at time t+1, we take the value at time t and multiply it by the weight. So if the value starts at 1 and the weight is 1.5, then the next value will be 1.5. Notice time here is in discrete steps (1,2,3,4, etc) like seconds on a clock.
The other kind of neural network is not recurrent, AKA feedforward networks. There are two important things to understand about feedforward networks. First, they are bounded in time (unlike recurrent networks). That means you calculate the first layer, then the second, etc, until you get to the end. If a feedforward network has 3 layers, you can think of it as giving you an output in 3 seconds or in 3 steps. Second, feedforward networks are basically funky regression with funky notation. If you understand regression, you understand a lot of what you need to understand neural networks.
Consider this feedforward network of 3 input nodes and one output node. How is this like regression? Imagine we are doing a regression where we want to predict weight using height and gender. In neural network notation, weight would be our output node, and height and gender would be our two input nodes. What about the 3rd input node below? That would be our intercept, or bias.
Under this example, the neural network is exactly the same as a linear regression. Each input node is the value of the variable and each weight from a node to the output is the coefficient of the regression. The intercept is a special case where we fix the input node to always have value 1 and the weight from it is the value of the intercept. Here's the equation:weight = w1*height + w2*gender + w3*1
You'll notice that instead of using b to represent the coefficients, I used w to represent the weights. w3 is the intercept.
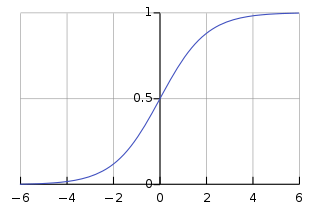
OK, fine, what about a classification task instead of a regression task (e.g. predicting gender from weight and height)? In that case we do exactly what we do with logistic regression: we run the output through a sigmoid function:
Now where neural networks start to get funky is when you add multiple layers. Consider the feedforward network below. The hidden layer (any layer between the input and output is called a hidden layer) has three nodes. Each of these nodes, with the three weights leading into it, is exactly like what we saw in the simple network above. In other words, we can view the hidden layer and input layer as three separate regressions fit to the same data.
In terms of equations, it would look like this:
h1 = w1*height + w2*gender + w3*1
h2 = w4*height + w5*gender + w6*1
h3 = w7*height + w8*gender + w9*1
where I've called the outcomes of the regressions h1, h2, and h3 with h for "hidden"; each h represents the activation of a hidden unit. As you can see, each "regression" here has its own weights. OK, let's now consider what the final output node of this network represents. Notice that the connections from the hidden layer to the output layer are exactly the same as our original network above, which we already mapped to a regression. So we could call this last layer "a regression combining regressions" and that would be mostly correct. Where it gets a bit off is that we don't have an obvious node representing the intercept. You can have regression with intercepts with certain assumptions, but let's put that aside for now.
So one way to think of neural networks with hidden layers is as a weighted combination of regression models (regression on top of regression). We've seen this kind of "ensemble" model before with bagging and random forests. A big difference is that those ensemble models were created by bootstrap sampling the data (i.e. created from individual samples of data) and then averaged, whereas the neural network is creating and combining the models all at the same time. Another big difference is that bagging/random forests have trees with arbitrary structures, whereas neural networks are forcing a similar structure across submodels.
There are three more things you need to understand about neural networks at this point.
The first is that because neural networks have this regular structure, people like to use matrix notation to describe them. Look again at my equations for the last network. You can see that the only thing changing is the weights, which have a rectangular shape. So I could have just written this as:
w1 w2 w3
w4 w5 w6
w7 w8 w9
And you can tell just by looking at it that there are three input nodes (three columns) and three hidden nodes (three rows). This is called matrix notation, and you can describe a feedforward network in terms of the weights between each layer. For example, The first layer might be W1 and the second layer W2 (which would be a 1 x 3 matrix). You can then multiply the input (a vector) by the weights (a matrix) to get the activation at a layer.
The second may not be obvious to you, but I'll try to explain and you can Google around if you're curious. It turns out that for neural networks to be more powerful than regression, they have to use something like the sigmoid in their hidden units. You will see that a lot, and there are many different ways of "squashing" the weighted sum of inputs. Why? Imagine you took two layers of weights without a sigmoid, i.e. just linear activations, and multiplied them together. You'd just get another weight matrix, and in fact, that weight matrix could then be used to replace the two you just multiplied together. If you think about this simply, starting with 1, adding 3, and then adding 5 is the same as starting with 1 and adding 8. Similarly, starting with 1, multiplying by 3, and then multiplying by 8 is the same as starting with 1 and multiplying by 24. When you multiply matrices, all you are doing is adding and multiplying the numbers in those matrices, so the claim that the resulting matrix can replace the two matrices isn't that surprising. However, as soon as you squash the hidden unit values between layers, this is no longer true.
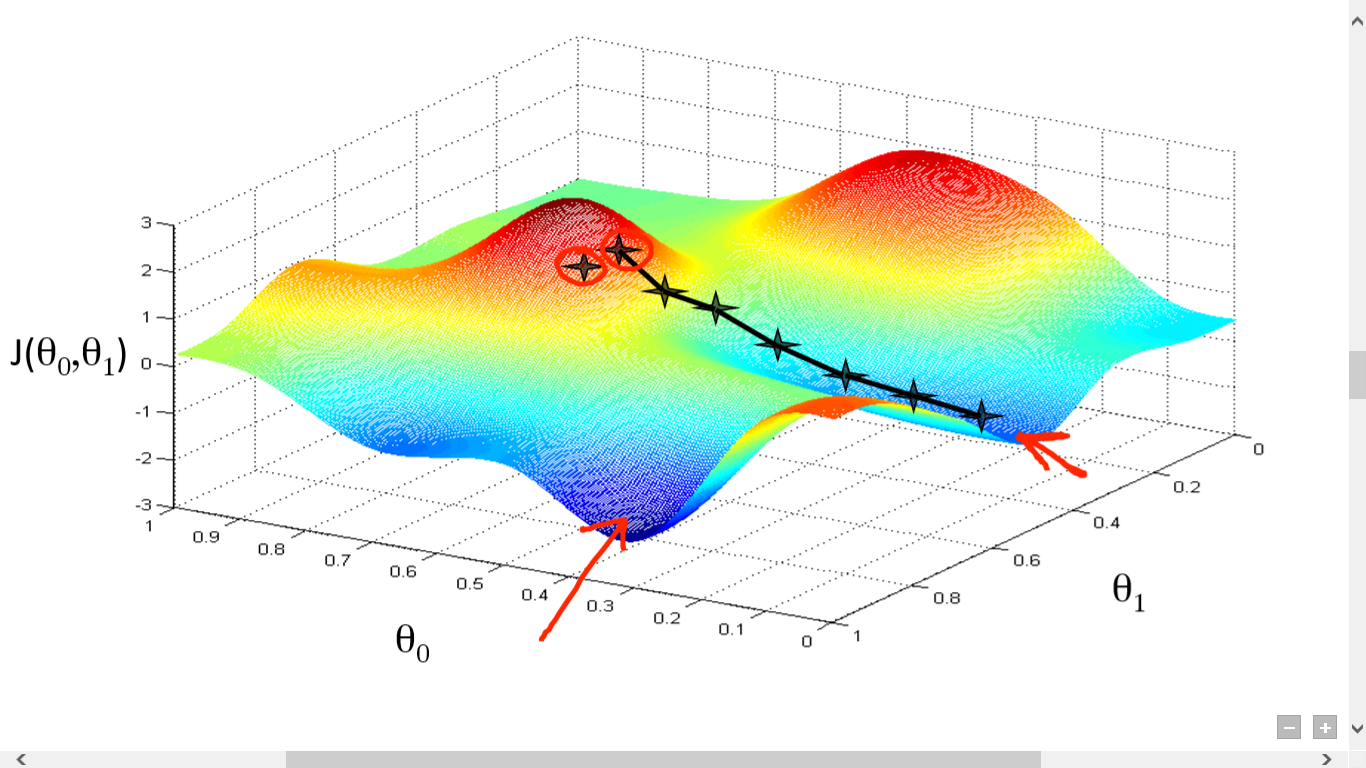
Finally, because they are so "funky," neural networks can't fit data (i.e. be trained) the same way as regression. Instead, they iteratively change their weights using the error at the output layer which is then propogated backward through the network (backpropogation). For example, if for a particular data point our output weight (using the age/gender example above) was 130 and it was supposed to be 120, then we have an error of 10 and we need to adjust the weights to make this error lower. This turns out to be complicated when you have multiple layers and many weights -- there are many things you could change. The way this is done is by using something called gradient descent (which requires calculus) but you can understand it without calculus. Imagine that you are on a foggy mountain and you are trying to find your way down. You can only see the ground right around you and it is sloping downward in one direction, so you decide to go that way. This is what gradient descent is doing. It is using local information about the gradient of the error surface to chose a direction and sometimes also a step size. Moving in that direction means changing the weights of the network accordingly. Once this is done for the output layer, the process repeats for each hidden layer until the input layer is reached. Here is a picture of gradient descent in action:
Hopefully this will be enough background for you to understand the readings :)
Banerjee 2013 & Banerjee 2014
ReplyDeleteBoth of these articles addressed the concept of the SELP (Surprise → Explain → Learn → Predict) framework and its relevance to Artificial Intelligence and Big Data. I found the arguments for this type of framework compelling. Banerjee 2013 states “in order to live in this world, the primary goal of an intelligent agent is to be able to discover coherent spatiotemporal objects at the highest level of abstraction from sensory data in different modalities using all available resources (p.2).” Deepening the argument even further, Banerjee 2014 explains the “never-ending tsunami of data (p.41)” and the imperative need “for a smart memory to learn the norms in such data so that only the abnormal (or salient) events may be stored (p.41).” The author’s solution, SELP, is based on “data-driven biologically plausible deep learning framework that gives rise to a smart memory system (p.41).” The author also gives a compelling argument about the importance of time when looking at this plethora of data and how an algorithm of this type could reduce the need for significant manpower. These concepts are all intuitive and convincing arguments for the need and usefulness of SELP. The methods described in both articles seem to be strong arguments for the model’s success. My main question, however, has to do with how this is actually used in real life. I think I get the concept for the most part and understand why it is useful, but how is it used or how can it be used? What are the most important implications of this model? Has it been implemented? The author claims in Banerjee 2014 that “SELP framework bears the potential to make significant breakthrough in the Big Data problem (p. 58).” How much of a problem is Big Data? Where is the problem the most alarming and/or concerning? I understand that the vast amounts of data make it impossible to explore all of it but is that always a problem?
Banerjee 2013:
ReplyDeleteI am uncomfortable with the assumption—common as it is—that neural architecture reproduces the world in miniature. This is the representationalist story of cognition. The word ‘representation’ means a lot of things across the cognitive sciences, surely. Neuroscientists usually just mean by that term a kind of statistically regular firing pattern associated with a given stimulus. But this paper uses a more robust and metaphysically charged concept of representation, as is more common in AI literature. My worry is that, while representational modes of cognition might be useful for creating AI agents, they may not be evolutionarily sound. The vast computational power and energy required for creating and continually updating internal models of the world is at least implausible if we don’t start with human agents, but instead start with simpler (=less degrees of freedom) biological agents: e.g., mollusks, snails, frogs, or hummingbirds. While I would never want to a priori rule out the possibility that a robust representationalism can explain these more basic minds, I at least think the representationalist has some explaining to do. For example, bivalve neurology is not even quite a brain. It’s more like a loose network of neurons and ganglia. But, let’s go to good old William James, who never gets old: “The pursuance of future ends and the choice of means for their attainment are thus the mark and criterion of the presence of mentality in a phenomenon” (1890/1950, p. 8). We might say, intentional behavior with some degrees of freedom are the mark of mentality—something beyond pure mechanical reflex. Bivalves do have minimal forms of intentional behaviors, including reproductive, nutritive, and escape behaviors. They also have minimal forms of perception and action. These kinds of minimal minds are the evolutionary history of more complex ones, like cephalopod minds (cephalopods being mollusks). It is, I suspect, too expensive (in terms of processing power and energy expenditure) for these minimal minds to represent the world. But you can scale this problem up, because this is where minds come from. Perception and action loops are the most basic forms of cognition, found across the board of neurological complexities, so their origin ought to be pretty inexpensive in terms of processing power and energy expenditure. This is why I think the ecological psychology and enactivist stories are more plausible—that perception is direct in the world and nonrepresentational. Certainly, there are more ecological and even nonrepresentational versions of predictive coding out there (e.g., Andy Clark, Shaun Gallagher). In short: what works for AI agents should not necessarily be assumed to translate simply into what happens in biological agents.
Banerjee 2014:
I’m definitely interested in predictive coding and this is a novel take on that (like the previous paper). I would be very careful in assessing any claims that this model is biologically plausible, however. As Antonio Damasio has forcefully shown us, the original sin of cognitive science is to separate affect from cognition. I think there’s a lot going for the predictive paradigm, but salience in biological agents must include affective salience. Biological things feel stuff, and feeling stuff drives behavior and is even part of what cognition is, to put it vulgarly. So, I like this paper, but hesitate before any claims of biological plausibility.
Considering neural networks in general, acknowledging the information about neural networks included above, and not being heavily educated in the realm of neural networks, in talking about the different types, are recurrent networks less commonly used/less complex than feedforward? or is it just a matter of whether or not they are bounded in time and how many layers are involved? Now,
ReplyDeletebased on both of Banerjee's articles, compared to previous types of neural network frameworks, overall, it seems as though the SELP has implemented beneficial attributes that can eliminate some of the problems faced with big data, or at least the author is confident that the framework has the potential to. He mentions and emphasizes that one of the desired attributes is to learn in an unsupervised manner. Have bigger machine learning mechanisms been created that are able to do this? Or is that one of the abilities that makes the SELP stand out among other similarly created frameworks? in section 1.2 of the 2014 article Banerjee specifically states “if algorithms can be developed that can analyze and learn effectively from unlabeled data without human intervention, it would significantly lessen the need for skilled manpower”—after this statement, it’s like he just shrugs it off—I kind of feel like this is a really bold claim, one that has many implications. I would be interested to hear him elaborate on this.
As they have tested this framework on different modalities, I wonder what the limitations have been/what flaws they have come upon? It didn’t seen like they focused on this in the article, rather the strengths and gains but I would presume that it had its shortcomings. With any type of research/complex design comes its limitations and I think lack a lack of acknowledging those hinders improvement.
The neural framework presented in these articles clicked with me on many levels because of several interesting emergent parallels to some properties of human cognition that I haven’t seen come through in previously discussed models. Due to the construction of this framework, it seems like a few things are taking shape similarly to some well know cognitive processes. For example, the structure of surprise combined with the spatiotemporal difference highlighter allows for “all computational resources to be deployed for learning from a small but more interesting space of the data,” which sounds a lot like it fits most models of attention and dual processing. Similarly, the way that the simple and complex sublayers interact (especially allowing more complex layers to dictate tasks of explanation to simpler layers) depending on the surprisal present of certain layers seems to resemble the top-down and bottom-up processing strategies of human cognition, despite not being explicitly built into the framework. Banerjee states humans tend to learn how to recognize environments without explicit teaching, so it seems that this framework is achieving its goal using similar emergent strategies, but does that also make it subject to similar weaknesses as human cognition, such as being subject to illusions, attentional blindness, and Gestalt influences? Further, what do we make of these similarities? Are they useful models of our own cognition, or are they just pleasant surprises that tell us that we’re on track?
ReplyDeleteAdditionally, there are many ways for this framework to intake data, from a wide variety of sensory inputs to reward and punishment data. However, since this framework is constructed with the purpose of flexibility and the lack of specific programming, how could in incorporate goals? In human cognition, our goals constantly influence the evaluation of surprising inputs and the nature of the explanations we use to incorporate them into our knowledge structures. Could the SELP framework develop goals given its ability to adapt to different reward systems (which could be a rudimentary description of a goal)? If so, how does this begin to influence the framework’s own decision-making? By extension, could certain goals either help or hinder the overall flexibility of the architecture over time?
I swear I did not read your response before writing mine, but I'm glad to see someone had the same reactions (e.g., dual-processing and susceptibility to illusion, though I didn't talk about the erroneous side). The idea of goals, and a means to assess whether these goals are met or not is definitely interesting, and a "reward" system (or maybe just punishment and avoidance of it) seems like an interesting approach.
DeleteBanerjee 2013 explains that the brain runs a relentless cycle of Surprise, Explain, Learn, Predict (SELP) involving the real external world and its internal model. Our perceptual organs sample the environment at regular intervals of time to maintain a true correspondence between the real world and its internal model, the stimulus obtained a any sampled instant must be explained He compares the SELP predictive cycle and the SELP explanation cycle.
ReplyDeleteBanerjee & Dutta 2014 used the SELP framework in artificial intelligence memory with the inference that norms in data must be learned in order to store only the salient events. This is a very promising concept when addressing Big Data.
Banerjee (2013 & 2014)
ReplyDeleteBoth of these articles reflected the same network architecture and framework, so I am describing them both together. I cannot speak to how well this works computationally (e.g., the efficiency of this approach relative to others), but the architecture underlying this system impressed me. Banerjee states in the papers, and his bio, the desire to align these models with human brain functioning, and I felt this was done very successfully. For example, in both papers he shows the most meaningful features represented by complex neurons, and the simple neurons that underly these features. It looked quite similar to the visual cortex functioning (based on a declining memory for my Sensation & Perception undergrad class). There are on-center/off-surround and off-center/on-surround features, which resemble retinal ganglion cells. Similarly, it built features representing columns at different orientations and many other brain-like features, especially in motion detection.
I’m curious if additional layers could be added to this, such as a “term” layer that is added above the complex layers to give meaning in some sense, such as identifying all variants of “7” as 7 (note: not that it UNDERSTANDS the layer, but that it knows that in spite of variation, all these things are one unified concept). In general, I would be interested to see if more layers could be added, or multiple modalities concurrently processed (e.g., video with audio), and how this could be built up. As it stands, I feel this is a beautiful representation of the sensory systems of the brain.
I’m also curious to see if this could be developed into a greater model of multi-modal information processing, to build a higher-level AI (e.g., that can read handwriting and learn from the words it extracts, expressed as applying the conceptual information from the writing to solve a new problem). I believe his emphasis on giving processing priority to unexpected events through prediction errors also brings this much closer to human cognition (e.g., attention). In the human brain, we have mechanisms like the dorsal-anterior-cingulate-cortex, which serves as a conflict detection region allocating more conscious processing resources (i.e., System 2 processing, in dual-process terms), and dopamine, which monitors rewards and reward-prediction-errors which, when encountered, can lead to greater processing or memory (though DA serves a lot of functions in many places, and my understanding is less clear).
Banerjee (2013)
ReplyDeleteLike others have noted, I find the SELP (surprise, explain, learn, predict) models of both the prediction and the explanation cycles to be interesting. Since this is my first exposure to deep neural networks, I think that it was helpful for me to have this acronym to think about these cycles in terms such as "surprise" and "learn" rather than "unexpected inputs" and "activation of higher layer neurons" because it seems more colloquial and a bit less intimidating to learn about. I thought it was very interesting that this SELP model, compared to ones we have previously discussed, doesn't constantly learn and save that data - learning occurs only when a predictive error, or a "surprise", occurs. I thought the explanation for this, so that the model can concentrate its resources on more interesting things, is pretty intuitive and similar to how people may learn through trial-and-error. I know there have been many times I've completed tasks the same way over and over until it fails and I'm forced to improve how I am doing things, which seems to be what this model does. Has the SELP model been implemented by any other researchers? Is it something that is, in fact, useful and should be used?
Banerjee (2014)
We've talked a few times about the actual, huge, vast amount of data that is being collected daily, not all (or mainly) by researchers, companies, and technology. Banerjee & Dutta address this issue with their solution to not store the data that is normal, but only when it strays from the normal - the SELP model. I was glad this paper expanded on just the photographic examples of the 2013 paper, showing how the model can be used more broadly with more types of input data. I found the concept of motion tracking coming from the neurons' inability to predict fast/constantly changing images to be interesting, as well as the predictions of auditory information of speech. I am looking forward to seeing what updates on the SELP framework Banerjee has to tell us about, and learning if it is being implemented in other research/other AI technology.
I found both of these articles to be interesting, especially as I have had very little exposure to deep neural networks previously. As other comments have mentioned, I think this approach is especially interesting in how they are attempting to model after human learning through use of the SELP model. I wonder if, at some point in the future when we have gotten closer to AI with human-level intelligence, if systems like this could be used to evaluate the effectiveness of teaching methods. If we could build a system that "thinks" like a human brain, we could theoretically then build a model that "thinks" like a brain of someone with a learning disability, allowing for strategic methods to be developed to best teach those individuals. The massive amounts of data generated in today's world could allow us to understand how people learn not just in classroom settings, but in all activities that they do, which could also be used to help guide instructional methods.
ReplyDelete
ReplyDeleteHow can the Blind Men see the Elephant?
What is horizontal hypothesis? Is this guy trying to build a robot that can understand human speech? Is ignoring gestures the right strategy? The author used a program called SELP to learn the neural architecture from space and time data. SELP stands for Surprising, Explain, Learn, Predict. How does SELP learn from correlations? Can you give an example of iconic and echoic memories?
SELP: A general-purpose framework for learning the norms from saliencies in spatiotemporal data.
The authors present a more detailed version of SELP that takes data from real world space and time data. How big of a role have real neurons and brain structures played in the development of SELP? Do the people making the SELP program and other neural networks consult with neuroscientists? I thought it was very interesting how they were trying to train a computer to see and hear the world similar to an animal, from the ground up.
Banerjee (2013)
ReplyDeleteThe SELP model is interesting and analogous to the cognition process. I think the text of prediction cycle and explanation cycle is reverse in Figure 2. Another question is about the example in Figure 3. The writer said that the image of Barbara was suddenly changed to that of Lena at t=50 while the t=50 is still the image of Barbara which makes me confusing. It seems that t=51 has a clearer image of Lena than t=52. I think I am curious about when the surprise comes out, how will the model deal with the surprise and the previous information? Can the new surprise combine with the old information?
Banerjee (2014)
I think maybe I have a wrong understanding since the figure 1 has the same text of explanation cycle and prediction cycle. The SELP learns the norms or invariances from saliencies or surprises in the data. I have a question about the prediction. Can the SELP use probabilistic machine learning in the prediction? For example, 3 may be similar to 8 due to the low pixel. What will the SELP do with this situation?
Banerjee 2013
ReplyDeleteI really like that the model described in this paper seems to be more closely modelled after human cognition than many neural networks that I have seen. The SELP model makes a lot of sense considering how humans learn, particularly in modeling lower level to higher level features. It’s very interesting that several phenomena such as something akin to human attention, that is diverting computational resources to learning a smaller, more interesting space, as well as something akin to human memory, that is, higher level features abstracted from correlations of lower layer activations that can give rise to something like iconic and echoic memory like when the “ghost” of one image was present and slowly faded, can all arise out of the neural network paradigm. I am curious as to at what point integration of systems such as these could give rise to human or superhuman intelligence. I think just a raw perception system, even one that learns, will likely not break that barrier, but is it merely a question of degree and ability in a single system? Or is there some necessary combination of many distinct systems each that gets at some phenomena of intelligence that are pieced together to make the whole?
Banerjee 2014
Also discussed in the previous paper, but explained in more detail here is the importance of lateral connections/weights between neurons in the same layer. In my little experience with neural networks, I have actually not seen this before, but it makes sense for learning along a spatial dimension. It was also interesting that in implementing the SELP framework, what assumptions were made for reconstructions in the architecture, namely: learn only from salient stimuli, learn an overcomplete dictionary, learn hierarchy of dictionaries, and predict the next stimuli. I wonder what other assumptions could be made, and what that would do to the speed of reconstruction. I would definitely like some clarification about simple vs complex neurons. So, is it the case that simple neurons are simply for learning spatial features (ie pictures), while complex neurons are a necessary component for processing spatiotemporal features (ie video)? Obviously both seem necessary to processing something like motion or video, but are both also necessary for processing static images? Additionally, how does the higher level of the neural network actually model higher level processing? It seems to be by some integration of information from the lower level neurons, but this is something that is also not entirely clear to me.